Here are the csound orchestra and score files and a sound file for the electronic part of Larry Polansky’s Horn.
horn-csound – csound orc and sco files
soundfile

Here are the csound orchestra and score files and a sound file for the electronic part of Larry Polansky’s Horn.
horn-csound – csound orc and sco files
soundfile
James Tenney composed For Ann (rising) in 1969 and made several realizations with tape and signal generators. In 1991 I was asked to engineer a compilation of his early computer and electronic music, “Selected Works 1961-1969”. Instead of using one of the tape versions of For Ann (rising), we decided to realize it digitally in Csound. Jim described the piece to me over the phone. The piece consists of 240 sine wave sweeps, each of which lasts 33.6 seconds long and rises 8 octaves (4.2 seconds per octave). Each sweep has a trapezoidal amplitude envelope which rises from 0.0 to 1.0 gain in the first two octaves, stays at 1.0 for the 4 mid octaves, and drops from 1.0 to 0.0 for the top two octaves of each sweep. A new sweep starts every 2.8 seconds. The initial Csound orchestra and score was simply:
sr=44100 kr=44100 ksmps=1 instr 1 kf expon 40, 33.6, 10240 ka linseg 0, 8.4, 2000, 16.8, 2000, 8.4, 0 a1 oscil ka, kf, 1 out a1 endin ---- f1 0 16385 10 1 i1 0 42 i1 2.8 42 i1 5.6 42 and so on.....
The tuning difference between each successive sweep is a 12tet minor 6th.
For the final version on the CD, Jim asked me to extend each sweep by 4.2 seconds (1 more octave). We moved the start point to A0 (27.5 Hz) – the end of each sweep is A9 (14080 Hz). This increased the length of the piece slightly 240 * 2.8 + 33.6 + 4.2 = 11:49.8.
I have recently put together a new realization of For Ann (rising) in Pure Data. I am using metro, delay and vline to generate the sweeps in this version, as these objects (unlike many objects in PD) are sample accurate, and should give consistent tuning accuracy. Also for this realization, I have added the capability to perform the piece with the original 12tet minor 6th, a just 1.6 ratio, and a golden mean (phi) ratio between successive sweeps.
The PD patch is available here, for those who want to hear the piece.
Here are the slides from my presentation on designing the Erbe-Verb.
Impulse Responses from various delay lines, in various states of repair –
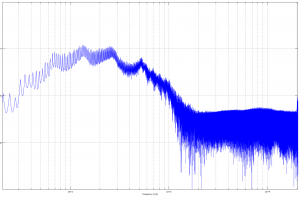
Gibson GA-4RE (Telray Adineko echo). This circuit has considerable leakage of dry signal. You can hear that as the first impulse. The first “dark” impulse can be considered the impulse response of the delay. Also, there is no erase “head”. The brush simply writes over the charge on each rotation of the disk. The repeated echo isn’t due to feedback, but progressive erasure. Use the entire impulse response for an accurate emulation.
Echoplex (Original – pre “EP-1” Serial 709). A tiny bit of dry signal leakage. The tape impulse response shows up at about 360 ms. I am not sure why there is a sine sweep artifact in this IR (after the impulse). Possibly because the tape transport is so unstable, or perhaps interaction with the bias oscillator?
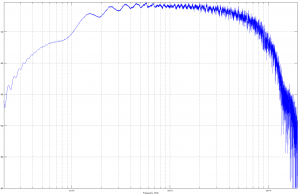
Roland Space Echo RE-201. Much cleaner compared to the previous two devices. No way to turn the dry signal off (perhaps my Space Echo is in need of repair?).
UPDATED – New measurement from the PA input to get just the tape signal (no dry)
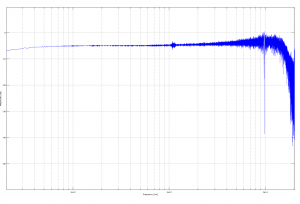 DeltaLab Effectron. A very clever digital delay which measures differences between successive samples. An almost flat response which tilts slightly upward.
DeltaLab Effectron. A very clever digital delay which measures differences between successive samples. An almost flat response which tilts slightly upward.
Bright Analog Delay Pedal. A modern CCD (charge-coupled device) delay. There is a bit of ripple in the passband (could be a Chebyshev I filter?) which caused a noticeable resonance after multiple repeats.
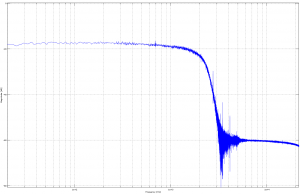
Dark Analog Delay Pedal. Another CCD delay. This one has a rounder, smoother filter response (possibly Bessel?), so no coloration after multiple repeats. Sharp rolloff at 2k for CCD aliasing rejection. You can see the signal leakage as a -60dB signal above 3k.
The sine sweep and golay code methods of impulse response measurement used are from Edgar Behrdahl & Julius O Smith’s Transfer Function Measurement Toolbox
A PD echo patch with convolution in the feedback
download this: emuplex
here’s an example of using clone to make a partitioned, low latency (256 sample) convolution..
Some abstractions for everyone to play with: max-reverb
I have completed porting 7 of 11 of my previous Max externals to the Max7 format as 32/64 bit universal macOS externals. This is beta software, so if any of you would like to try them, I would enjoy feedback (error messages, crash reports) if they don’t work on your machine.
If you would like externals for earlier versions of Max – please check the freeware section of www.soundhack.com
Paper: The Computer Music Realization of John Cage’s Williams Mix
[bandcamp width=100% height=120 album=3410817600 size=large bgcol=ffffff linkcol=0687f5 tracklist=false artwork=small]My current files for the performance version of John Cage’s “Williams Mix” can be downloaded here:
WilliamsMixPD201607
To run this patch, you will need the following PD externals:
– knob, within the flatgui distribution
– shuffle, within the motex distribution macos, windows and linux
– +binaural~, within the soundhack distribution (scroll down)
A sample sound file library is included here:
wmsounds
The sound file folder will need to be in the PD path. Once that is set, you can open wmmain.pd. It will seem to freeze, but it takes a while for PD to load 600 sounds into memory. If you do not have enough RAM in your computer, the piece may crash.
To run the piece, click “Open” to open the score file, click the number corresponding to your speaker format (2, 2 binaural, 4, 6 or 8), and click play. The piece is 4:15 long. There is a button on the upper right which will “shuffle” the file choices for each subcategory. This should only be done when the score indicated the piece is “mobile”. This is my interpretation of Cage’s score as applied to this computer arrangement.
Using your own sounds
You will want to collect new sounds if you wish to create your own performance of the piece. You will want to consult Cage’s instructions for the sound collection (about 500 sounds in 6 categories are required). You will need to use 44.1k, monaural, 16 bit wave files to be compatible with this piece. Place them in folder which is in the PD search path.
Edit wmfileopen.pd, creating a “wmtable bird2.wav” for a soundfile named bird2.wav. Repeat for each of your sound files. This may take some time!
After this, you will need to modify the random sound selectors wmfileloadA.pd, wmfileloadB.pd, wmfileloadC.pd, wmfileloadD.pd, wmfileloadE.pd and wmfileloadF.pd. This means repopulating the selection tree for each of Cage’s 48 subcategories. The selection symbol will match the sound file name. Again, a time-consuming process.
Notes
It will take a lot of work and some PD expertise to use this computer realization of Williams Mix.
I am supplying this patch purely for educational and research purposes.
Patches demonstrating several types of reverb (Schroeder, Moorer, Moore, Gerzon, Dattorro).
I was just looking over the structure of “Williams Mix”. It is divided into 11 sections that repeat a rhythmic structure 5 6 16 3 11 5. In section 4, the 3 subsection is one inch short. I imagine when they were calculating tape start times for editing, they forget to carry the one. The 16 subsection is based on a 10.25 inch length, so is 164 inches. It starts at 1129.75 inches and ends 1293.75 inches. The 3 subsection is also based on a 10.25 tape length, so should be 30.75 inches. However, it ends at 1323.5 inches: 1323.5 – 1293.75 = 29.75. Earth shattering news?
So the piece shouldn’t be 4:15.8, but 4:15.866666…